RADAR CHART POWER (RC-POWER)®は、平均とバラツキが一元化されたひとつの値であり、バランスよく得点が高いかどうかを示します。
RC-POWERについては、RADAR CHART POWERをご参照ください。
健康は、運動、栄養、休養の3つの要素でとらえられ、健康になるとは、この3要素のバランスを整えることといわれています。このように、私たちは、状態を複数の項目から調べ、それらの評価をまとめて、その状態をとらえようとします。
同じように、例えば学力も数学、国語、理科、社会、英語の5教科から推し測ろうとします。表1に示す5教科の点数を例にして、総得点とRC-POWERで学力の推移をみてみましょう。
表1 各教科の得点(100点満点)
| Aさん | 1年次 | 2年次 | 3年次 |
|---|---|---|---|
| 数学 | 80 | 60 | 70 |
| 国語 | 40 | 70 | 70 |
| 理科 | 70 | 60 | 80 |
| 社会 | 80 | 100 | 60 |
| 英語 | 60 | 70 | 80 |
総得点でまとめる
総得点はなじみ深いまとめかたですが、点数のバラツキを推し測るには、平均点、標準偏差が必要です。それらも含めて、各学年次での得点を表2にまとめます。
表2 各学年次での総得点、平均点、標準偏差
| Aさん | 1年次 | 2年次 | 3年次 |
|---|---|---|---|
| 総得点 | 330 | 360 | 360 |
| 平均点 | 66 | 72 | 72 |
| 標準偏差 | 15.0 | 14.7 | 7.5 |
1年次から2年次で総得点が増え、2年次から3年次では、総得点(平均点)は変わりませんが、標準偏差が小さくなっていることから、教科のパラツキが緩和され、学年が上がるにつれて均衡のとれた学力へと向上したことが窺えます。
図1は、表1の得点の積み上げ棒グラフです。このグラフからでも、均衡のとれた学力への推移は読み取れます。
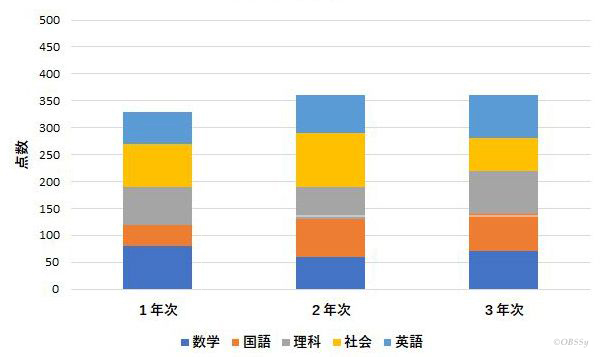
図1 総得点の推移
このように、総得点でまとめ、平均点と標準偏差を加えると詳しい情報が得られます。
RC-POWERでまとめる
この例を各学年次の特性を一目でとらえるために、図2に得点をレーダーチャートで表示しました。すると、1年次から2年次で5角形が大きくなり総得点が増え、2年次から3年次では5角形の形が整い教科の均衡がとれたことが推察されます。レーダーチャートの形状変化を観察しても、均衡のとれた学力への推移が推察されます。
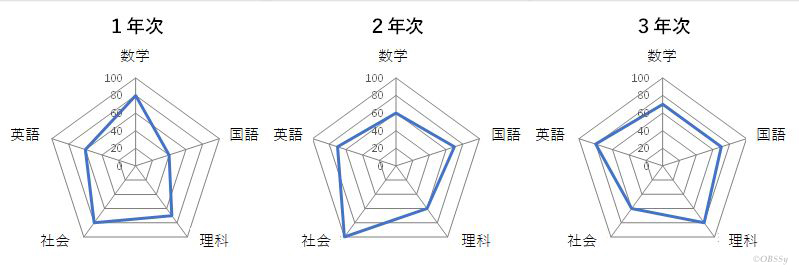
図2 レーダーチャートでみる学力の推移
各学年次のレーダーチャートに対してRC-POWERを計算すると、1年次 59.81% 2年次 67.29% 3年次 71.22%となりました。点数と%で単位は異なるものの同じ値域をとるため、比較のため、表2の平均点と標準偏差による誤差範囲とともに、図3に示します。
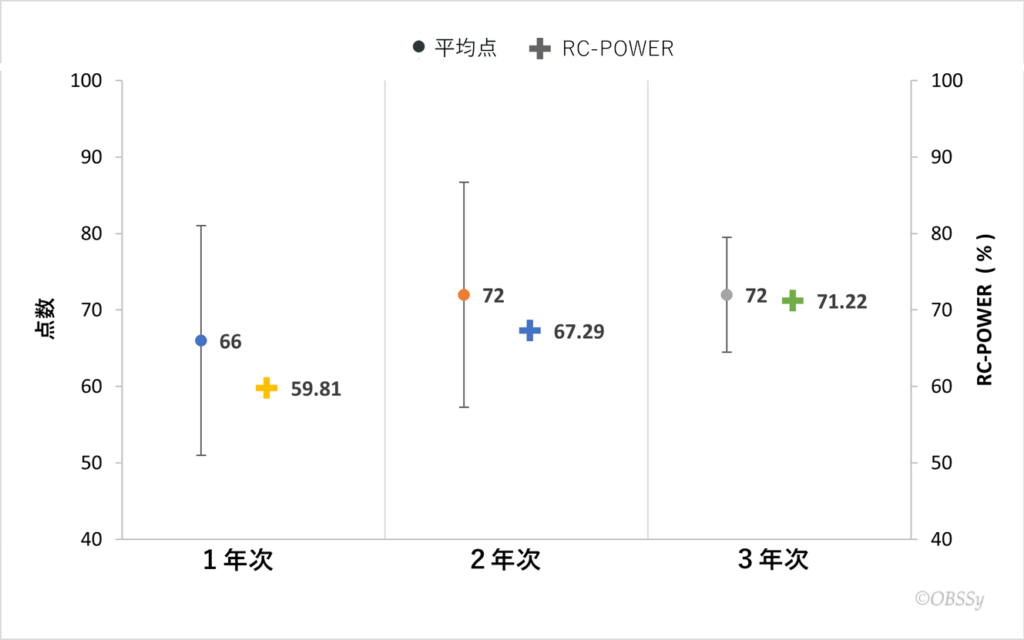
図3 RC-POWERと平均点・標準偏差でみる学力の推移
1年次から2年次での平均点の増加、標準偏差の減少は、RC-POWERでは59.81%から67.29%への増加となっていますが、どちらも標準偏差が大きいため、RC-POWERは平均点を大きく下回っています。2年次から3年次での平均点は変わらず、標準偏差は減少という変化は、RC-POWERでは67.29%から71.22%への増加となっています。標準偏差が小さくなったために、RC-POWERは2年次より大きくなっています。このように、RC-POWERは、平均点と標準偏差を一元化した値になっています。
まとめ
・ なじみ深い総得点では、バランスよく高得点かを知るには、平均点と標準偏差を調べる必要があります。しかし、RC-POWERはそれらを統合して、ひとつにまとめて示します。
・ RC-POWERは、平均とバラツキが一元化された指標であるため、総合評価が容易になり、判断の目安になります。
追記
バラツキを標準偏差で表すように、レーダーチャートでもバランスよく得点しているかに相当するレーダーチャートの歪みをRC-POWERで表すことができます。詳しくはお問い合わせください。お問い合わせはこちら
